The physics of knots

by Ben Crowell

This web page uses MathML to display equations. MathML is currently supported by Firefox but not Internet Explorer, so if you're using IE, the math will probably not look right.

There is a huge and active field of mathematics known as knot theory, but it has little to do with what sailors, mountaineers, and fishermen mean when they talk about knots made using physical pieces of cord and held together by friction. The analysis of these real-life knots has only been addressed in a very small body of scientific papers, which are not freely available on the web. The purpose of this article is to present a brief overview of this analysis, as well as a description of a few of my own experiments in which I've tried to test the theoretical predictions. My focus is on the question of whether a certain knot will slip, not whether it will fail because the rope breaks. For a discussion of the latter, see [Pieranski 2001], which includes both detailed numerical simulations and clever experiments using strands of spaghetti!

Bayman's theory of hitches

The classic paper is [Bayman 1977], which presents a simple theory of hitches. For simplicity, only the frictional forces between the rope and the post are taken into account; friction of rope on rope is assumed to be negligible. The advantage of restricting the discussion to hitches is that the rope conforms to the circular post, so that the geometry is known, stable, and relatively simple. Figure 1 shows a clove hitch. In a typical real-world application, such as tying a boat to a dock, the standing end is counted on to hold its load even when the tension in the working end is small or zero.

If you're inclined to think that all the scientific analysis is a waste of time, you may wish to stop reading for a moment, take a piece of sewing thread, and use it to tie a clove hitch around your finger. You will find that the hitch always fails; this turns out to be because of the small diameter of the thread compared to the finger. People who use knots for practical purposes tend to use them in specific ways that have been taught from generation to generation because they seemed to work. But the mountaineer who ties a clove hitch around a big tree trunk as an anchor may be in for a nasty surprise due to the large size of the trunk compared to the rope.

Bayman's analysis of the clove hitch considers the tension in the rope at the five points shown in figure 2. The top loop of rope, 3, presses down on thes loop underneath, causing friction between the bottom loops and the post. In the first loop, this friction causes `T_2` to be greater than `T_1` by an amount that is proportional to `T_3`:

`T_2=T_1+uT_3` (equation 1)

If the friction is static rather than kinetic, then this is to be interpreted as the maximum value of `T_2`. My experiments with typical materials such as nylon have shown that there is no measurable difference between the static and kinetic coefficients of friction, and in any case the security of a knot should be judged according to the kinetic coefficient, not the static one: we don't want it to fail because it is momentarily disturbed enough to break static friction.

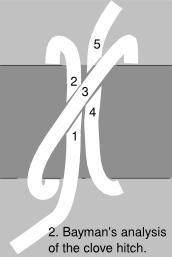
The constant of proportionality `u` in equation 1 depends on the coefficient of friction `mu` between the rope and the post, and also on the angle `alpha` formed by the slight kink in 3 as it passes above the lower loop. For example, when the ratio of the rope's radius `r` to that of the post `R` is small, and the crossover is isolated from other crossovers (which is not the case for the dressing of the knot shown in the figure) `alpha approx 4 sqrt(r//R)` (in radians), and `u approx 4 mu sqrt(r//R)`. In reality, it's not usually possible to predict the value of `u` accurately; we simply know that it increases with `mu` and with the ratio `r//R`.

As the rope passes around the back of the post from 2 to 3, its tension changes due to friction. A classic exercise in Newtonian mechanics shows that when a rope wraps around a post through an angle `theta` in radians (i.e., `n=theta//(2pi)` turns), the maximum increase in friction is

`(T')/T = e^(mu theta)` . (equation 2)

As in the analysis of `u`'s dependence on `mu` and `r//R`, this relation should not be expected to hold to high precision, even if, as is not usually the case, `mu` can be determined accurately. My own experiments show that there is usually a roughly exponential dependence on `theta`, but the rate of exponential growth may be much lower than predicted by this equation (it seems to depend on `r//R`). Presumably for this reason, Bayman instead takes

`(T')/T = epsilon^n` , (equation 3)

where `epsilon` is to be determined empirically, and `n` is, as above, the number of turns. In our example of the clove hitch, we have `n=1`, so `T_3=epsilon T_2`. Eliminating `T_3`, we now have

`T_2 = T_1/(1-u epsilon)` . (equation 4)

This equation applies to the case in which a load is applied to the knot, and friction is not preventing the clove hitch from holding. We find that there are two qualitatively different possibilities.

For `u epsilon lt 1`, these assumptions are self-consistent, and the segment of the knot from 1 to 3 provides some maximum amplification of any braking force applied at 1. This use of friction as a force amplifier will be familiar to climbers and mountaineers, who use a belay device to lower other climbers or arrest their falls. A small force on the brake strand translates into a much larger force on the load. In the example of the clove hitch, further amplification occurs between 3 and 5, and the total amplification can be easily found by further application of the principles already demonstrated.

For `u epsilon ge 1`, the assumptions made above are not logically consistent, and the infinite or negative result of equation 4 is unphysical. It is not possible for the knot to slip, even if the working end has zero tension and the load is infinite. Before the knot slips, the rope or some other part of the system will break. In this case, the only function of the second loop of the clove hitch (from 3 to 5) is to keep the bottom loop (1 and 2) from slipping out from underneath the top loop (3).

Bayman's analysis of hitches can be applied to any hitch without further ad hoc assumptions, depends only on the topology of the hitch, and gives a condition for the hitch to hold which can be restated as an inequality involving the determinant of a certain matrix. The same analysis is presented, with some interesting additional examples, in [Walker 1983]. A brief exposition, with almost no added material, is also given in [Kauffman 1991], which, despite its title, is not a book about physical knots made of pieces of rope.

Extensions to the theory

[Maddocks 1987] extends the analysis to take into account rope-on-rope friction and various geometrical complications. The effect of rope-on-rope friction does not lead to any qualitative change, for example, in the behavior of the clove hitch; the effect can simply be subsumed by increasing the value of the parameter `u`, which in any case (in my experience) cannot usually be reliably determined from physical measurements on the rope.

In freshman physics courses, students learn a standard model of friction between dry, solid surfaces, which dates back to Amontons and Coulomb in the early 18th century. Fishermen and mountaineers often tie knots in ropes that are wet, and the Amontons model is not necessarily accurate in this case. Even with dry ropes, my experiments have shown behavior that is not consistent with Amontons friction.

Amontons friction is velocity-independent, so applying the model to a system governed by Newton's laws, we generically predict motion with constant acceleration (which could be either zero or nonzero). In reality, experiments with a helical coil of rope wound around a post (as described by equation 2) often seem to give motion that either starts and stops erratically or, in some cases, flows at a small but constant velocity. Physically, such behavior can only arise from velocity-dependent friction, probably internal friction in the fibers of the rope. [Bedogni 2011] shows a very successful model of such viscoelastic friction in a dynamic mountaineering rope. Anecdotally, one hears stories about knots gradually "creeping," especially when they are tied in some of the modern high-strength materials such as dyneema (spectra), which have low coefficients of friction. Here is a video of a bowline tied in dyneema as it slowly flows apart. This type of behavior should give nightmares to rock climbers and mountaineers, and deserves to be studied more thoroughly.

Knots

It is much more difficult to make tractable models of knots that are not hitches. In their long paper, Maddocks and Keller make a brief excursion into an attempt at such an analysis. By making some ad hoc assumptions, they analyze two knots, the square knot and the sheepshank. The result in each case is a transcendental equation giving a certain critical value for the coefficient of friction below which the knot will fail. For the square knot, the equation is `1=2 mu e^(mu pi)`, and for the sheepshank `(1+mu)//2=e^(-2pi mu)(1-mu//2)`. They do not explicitly give the numerical solutions, which are approximately 0.24 and 0.09, respectively.

The only other prediction I've seen in the literature is the following claim by Kauffman: "The granny will not hold. No mutual interlock here. A pull facilitates a flow of rope through the knot's pattern until it is undone." Kauffman does not present any calculations to support this claim.

Here are the results of some of my own experiments:

material	`mu`	granny	sheepshank	square knot	figure-8 bend
teflon	~ 0.04?	fails	fails	fails	holds
dyneema	.05-.08?	fails	fails	fails	holds
rayon satin	...?	fails	holds	holds	holds
nylon	0.22+-0.05	holds	holds	holds	holds

These results are approximately consistent with the predictions by Maddocks and Keller for the square knot (but with a somewhat lower critical value for `mu`). The observations contradict the prediction that the sheepshank would be dramatically more secure than the square knot. The experimental results with nylon are not consistent with Kauffman's claim that a granny never holds (although it was necessary to dress and tighten the granny carefully to get it to hold).

Conclusions

Bayman's theory of hitches is simple, beautiful, and successful. It explains why some hitches have a regime of behavior in which they will not slip under any load, while other hitches never hold passively. For the hitches that have a non-slipping regime, the theory explains the physical parameters (`mu` and `r//R`) that determine when the knot is in this regime. It explains the behavior of many practical frictional machines, such as belay devices and brake bars. An understanding of the theory allows us to extrapolate from familiar conditions to unfamiliar ones, predicting, for example, that a clove hitch tied around a large tree will fail.

We don't seem to have a correspondingly successful theoretical model of friction knots other than hitches, so when it comes to these, the only practical guidance we have comes from centuries of accumulated experience -- i.e., folk wisdom. This folk wisdom doesn't apply to modern materials such as dyneema, and the best advice one can therefore give is to avoid ever tying any knot in these materials for a safety-critical application. Because of their unique combination of properties (low external coefficient of friction plus viscoelastic internal friction), their failure modes may be dramatically different from what one expects, e.g., constant-velocity "creeping" rather than rapid failure under load. Tabletop tests with loads applied with the hands may, for example, convince one that a triple fisherman's bend will hold in dyneema, but the results of such experiments may be misleading because the experimenter is looking for the familiar mode of failure rather than the actual one. Since the properties of these materials can be adequately characterized, there would seem to be no barrier preventing the construction of brute-force numerical models, which then might provide deeper insight.

References

Pieranski et al., "Localization of breakage points in knotted strings," New Journal of Physics 3 (2001) 10.10.13 http://iopscience.iop.org/1367-2630/3/1/310/fulltext/1

Bayman, "Theory of hitches," Am J Phys, 45 (1977) 185

Jearl Walker (Amateur Scientist column), "In which simple equations show whether a knot will hold or slip," Sci Am 249:2, p. 120, August 1983.

Kauffman, Knots and Physics, World Scientific, 1991. The analysis of physical knots made out of rope is at pp. 4-7 and 323-331.

Maddocks, J.H. and Keller, J. B., "Ropes in Equilibrium," SIAM J Appl. Math., 47 (1987), pp. 1185-1200.

Bedogni and Manes, "A constitutive equation for the behaviour of a mountaineering rope under stretching during a climber's fall," Procedia Engineering 10 (2011) 3353, http://www.theuiaa.org/upload_area/files/1/sdarticle.pdf